Guiding errors are inevitable, however they can be reduced to a minimum with the correct guiding hardware and strategy.
Although our ONAG® goes a long way for achieving very low guiding error, most people do not recognize how paramount is to correctly set-up and use an auto guiding software, you can find further information and useful tips on this matter in the ONAG®’s user manual.
One fundamental question one should ask, and eventually answer, for astro-photography is how much guiding error is too much?
From the answer to this question depends grandly the quality of the images. Each star on your frames shows the point spread function (PSF) of your system as well as the performance of the tracking and guiding.
Image inspection can reveal naked eye if the stars look right, tight and round enough. However using numbers to back-up this feeling is necessary to improve the performances, and eventually the image quality.
There are two good figures of merit for this task:
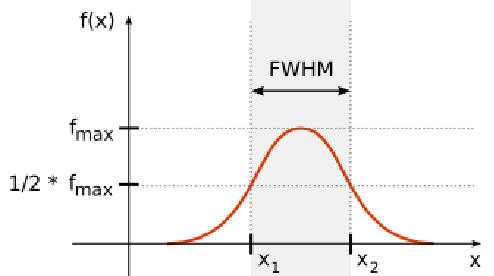
The FWHM (Full Width at Half Maximum):
The FWHM of star describes how much the star’s profile extends from its center. Most of the time, in order to compare between optical set-ups, this value is given in arc-second (“). The two plots below show the FWHM concept, on the left as a cross section of the star, on the right its 3D version.
Star Full Width at half maximum (FWHM)
A typical 2D star shape
The minimum FWHM is always bounded by either:
-1- From space the diffraction limit (airy disk, Rayleigh’s limit) expressed in arc-second (“) by:
FWHM = 0.0212 * lambda/D
Where lambda is the wavelength, in nm, under consideration (usually 550nm for the visible range) and D the scope aperture in cm.
For instance at 550nm a 30cm (12 inches) scope has a difraction limit of 0.0212*550/30 = 0.39″
In such a case we could expect to make the FWHM as small as we would like by choosing a large enough scope aperture D.
-2- From Earth the seeing limit (Gaussian like shape) expressed in arc-second by:
FWHM = 0.025*lambda/r0
where lambda is in nm and r0 in cm.
r0 is known as the coherence length of the atmosphere (Fried’s parameter). It typically stretches from 5cm to 20cm, with values up to 40cm, or more, in very good seeing conditions such as Paranal in Chili (ESO).
In average r0=8cm or so, yet its modal value (the most likely) is more in the 5cm to 6cm.
For instance the same 30cm scope with an average seeing has a seeing limited resolution about 0.025*550/8 = 1.7″. Which is like if the scope had an aperture 0f 8cm instead of 30cm.
Average seeing is around 1.5 to 2 arc”. Smaller the FWHM is tighter the star will look.
We are seldom diffraction limited, unless you have an exceptional site and some expensive piece of equipment (adaptive optics with an artificial guide star). Most of the time only professional astronomers can afford and expect seeing as low as 0.5 arc”, or less.
The roundness (RDN) of a star:
If the FWHM describes how a starlight is spread, or “fat” a star is, its roundness relates to how circular the star profile (shape) is, which is also very important for image appearance and quality.
If we consider, in first approximation, a star shape is like an ellipse (worst case), then a natural and classical definition for the roundness is simply given by how much longer the major axis is relative to the minor axis of the ellipse.
A RND of zero means the star is a circle indeed. It is expected that a RDN lower than 0.1 (or 10% of elongation) is not perceptible by most people.
RDN = (Major axis – Minor axis) / (Major axis + Minor axis)
In order to keep the RDN < 0.1 we need to make the guiding error small enough. Most of the time the error is much more on Right Ascension (RA) axis than Declination (DEC).
This is because the mount RA drive motor is always moving at sidereal speed (15 arc” per second) for compensating Earth rotation.
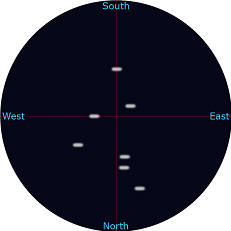
While with a good polar alignment the mount DEC drive motor seldom moves. The result is that guiding errors are more prone in the RA direction (East – West), as it can be seen on the left image below, a typical situation and symptom of a guiding problem in RA.
Guiding error is most of the time given and reported from most software by its RMS (Root Mean Square) value, the average deviation from nominal.
There is a link between the FWHM and the level of RMS guiding error we can afford to keep the RDN below the 0.1 (10%) threshold.
The parameter of interest for driving this being the local seeing FWHM assumed without any guiding error.
It seems logical to expect a larger RMS guiding error would be more acceptable when the local seeing is worse, and the other way around. After some calculations comes this simple rule of thumb* for achieving RDN < 0.1, or 10%:
RMS tracking error < 1/4 FWHM_seeing
Elongated stars
Recommended maximum RMS tracking errors

See the right table above for the maximum recommended rms tracking error versus the local seeing.
For instance for RDN < 0.1, with a local FWHM seeing of 2 arc” (average), a 2m scope focal length, and a 8 microns imager pixel size, one needs to keep the RMS guiding error at, or below 0.6 pixel, see below:
FWHM_seeing = 19 microns or 2.42 pixel
RMS error < 5 microns or 0.6 pixel.
1 micron = 4/100,000 inch
One does not need much to experience an error of this magnitude. It is why all aspects of the system must be considered, such a flexure, part motions (mirror, focuser play, …), mount tracking quality, auto-guiding software and set-up.
Our product offers a unique solution for a flexure and motion free system without any compromise on the image quality and a wild guider field of view. Also auto-guiding in NIR smooths tracking due to lower seeing effects, the guide star experiences much less wander this way.
* Assuming a normal RMS error probability density function in the calculation.
